GPS protocol#
The GPS protocol allows locating a device through mesuring its distance with other wireless devices which already know their position. It was probably introduced on ComputerCraft by BigSHinyToys (see the topic).
Protocol description#
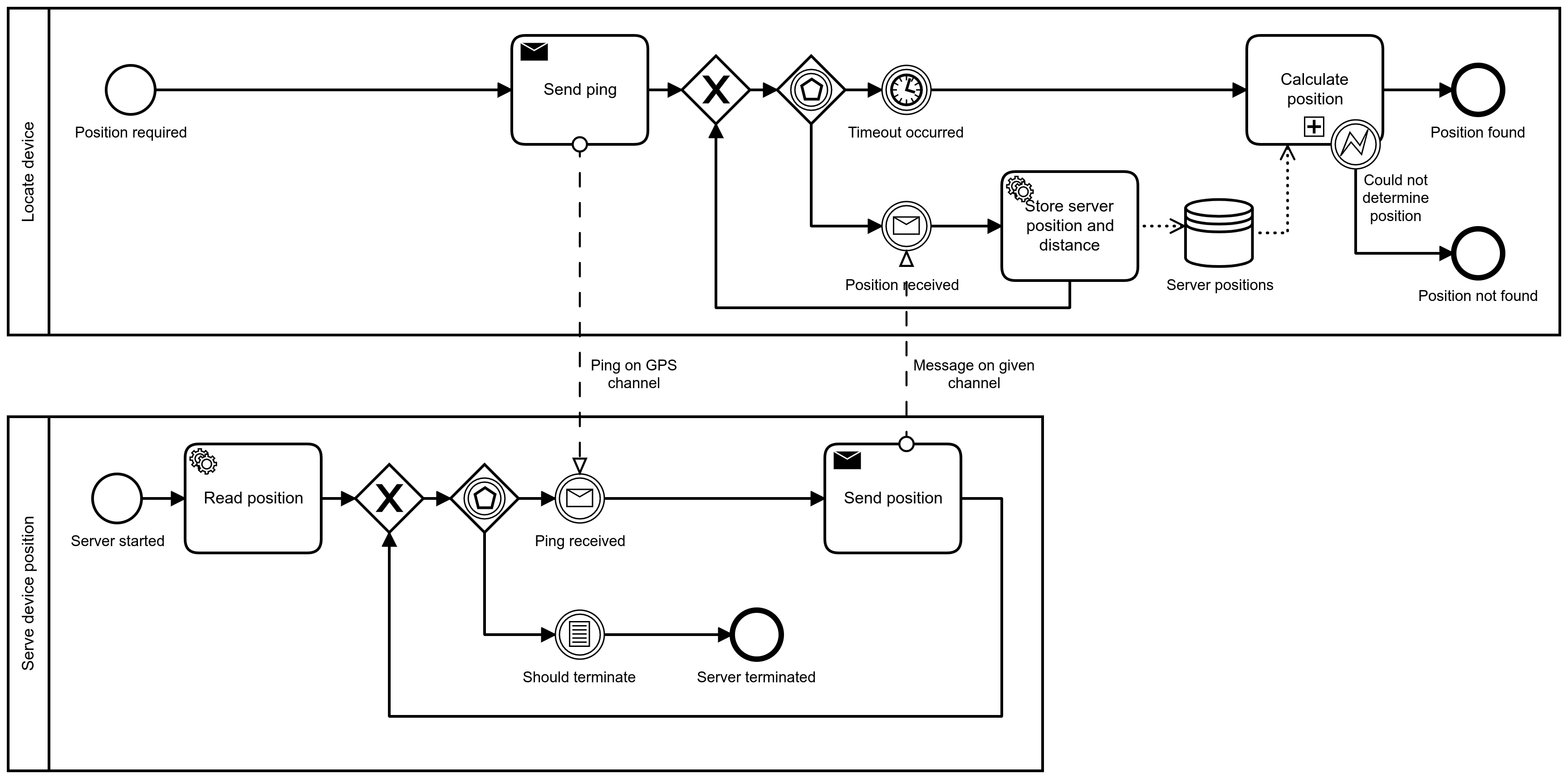
The protocol makes use of modem channel 65534, known in CraftOS as
gps.CHANNEL_GPS. There are two sides to this protocol:
Devices that don’t know their position yet, and want to find it out; these devices will be called “Client”.
Devices that know their position, and are able and willing to share it; these devices will be called “Server”.
Usually this protocol is implemented by having machines dedicated to sharing their position which must be in range of all other machines that want to know their position; however, a peer-to-peer approach can be taken, by allowing each device that knows their position to share it. This is the approach chosen in thox; however, note that some machines will require some devices to have their position set manually in order for the rest of the devices to find out theirs.
The protocol starts when the Client wants to find out its position. It then sends the string “PING” to the GPS channel, while giving a reply channel. This reply channel is usually the computer ID, like for Rednet.
Note
The fact that the reply channel is usually the computer ID is probably the reason why the dedicated page on the wiki of the ComputerCraft mod incorrectly states that the PING message is sent over Rednet while the message format doesn’t match. See this page for reference.
The Client then proceeds to listen for a given timeframe (by default, 2 seconds, although the duration of this timeframe is configurable in the native API).
During this timeframe, all the Servers who have heard and process the ping message send a geogebra-exportmessage back on the reply channel given by the Client, defining the GPS channel as the reply channel, as a sequence of three numbers containing, in order, their x, y and z coordinates.
An example implementation of this iteration from the Server on native CraftOS is the following:
local eventType, side, channel, replyChannel, message, distance = os.pullEvent("modem_message")
if channel == gps.CHANNEL_GPS and message == "PING" and distance > 0 then
peripheral.call(
side,
"transmit",
replyChannel,
gps.CHANNEL_GPS,
{x, y, z},
)
end
Every response from a Server is stored with the distance calculated by the modem peripheral. Once the timeframe has passed, the positions are taken and a position calculation is attempted at; see Trilateration.
Every response from a Server is stored with the distance calculated by the modem peripheral. Once the timeframe has passed, the positions are taken and true-range trilateration is applied to calculate the position.
The position calculation can fail for a few reasons, included but not limited to:
No or not enough server positions (at least three positions are required).
Ambiguous position; this could be due to insufficient precision or bad placement of the other devices.
Trilateration#
Classic GPS API implements the trilateration method in gps.trilaterate, using the separate vector library.
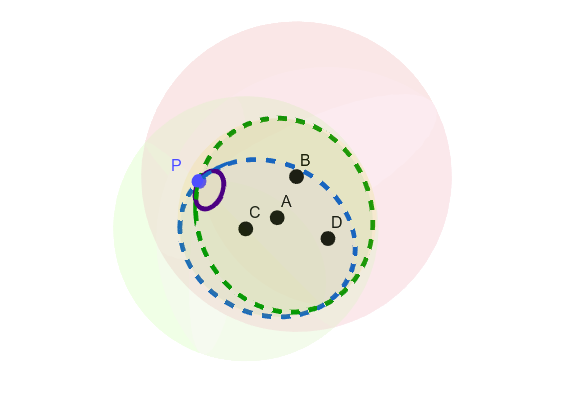
A view of the trilateration calculation as the intersection of four different spheres, where A, B, C and D are four GPS hosts, the four spheres using them and their distance to P as the radius, and P being the position of the device trying to locate itself. The intersections using A, B and C intersect in two points; using D (purple circle), we can eliminate one to find P.#
The position is calculated using true-range trilateration. The idea is the following:
If we have one GPS host, we are located somewhere within a sphere.
If we have two GPS hosts, we are located somewhere within a circle, intersection of two spheres.
If we have three GPS hosts, we are located in one of two possible points.
If we have four GPS hosts, we are located in a single point.
In order to calculate the coordinates of the two possible points using three GPS hosts, we will use the adapted Bancroft’s algorithm using vectors.
We start by placing ourselves in the \((A, \vec{E_x}, \vec{E_y}, \vec{E_z})\) three-dimensional marker, where \(\vec{Ex}\) is normalized \(\vec{AB}\):
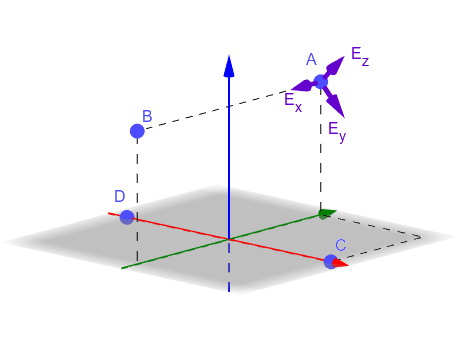
A visualization of the new marker, where \(\vec{Ex}\), \(\vec{Ey}\) and \(\vec{Ez}\) are defined as above.
This means that A has coordinates \((0, 0, 0)\), B has coordinates \((U, 0, 0)\) and C has coordinates \((V_x, V_y, 0)\), where:
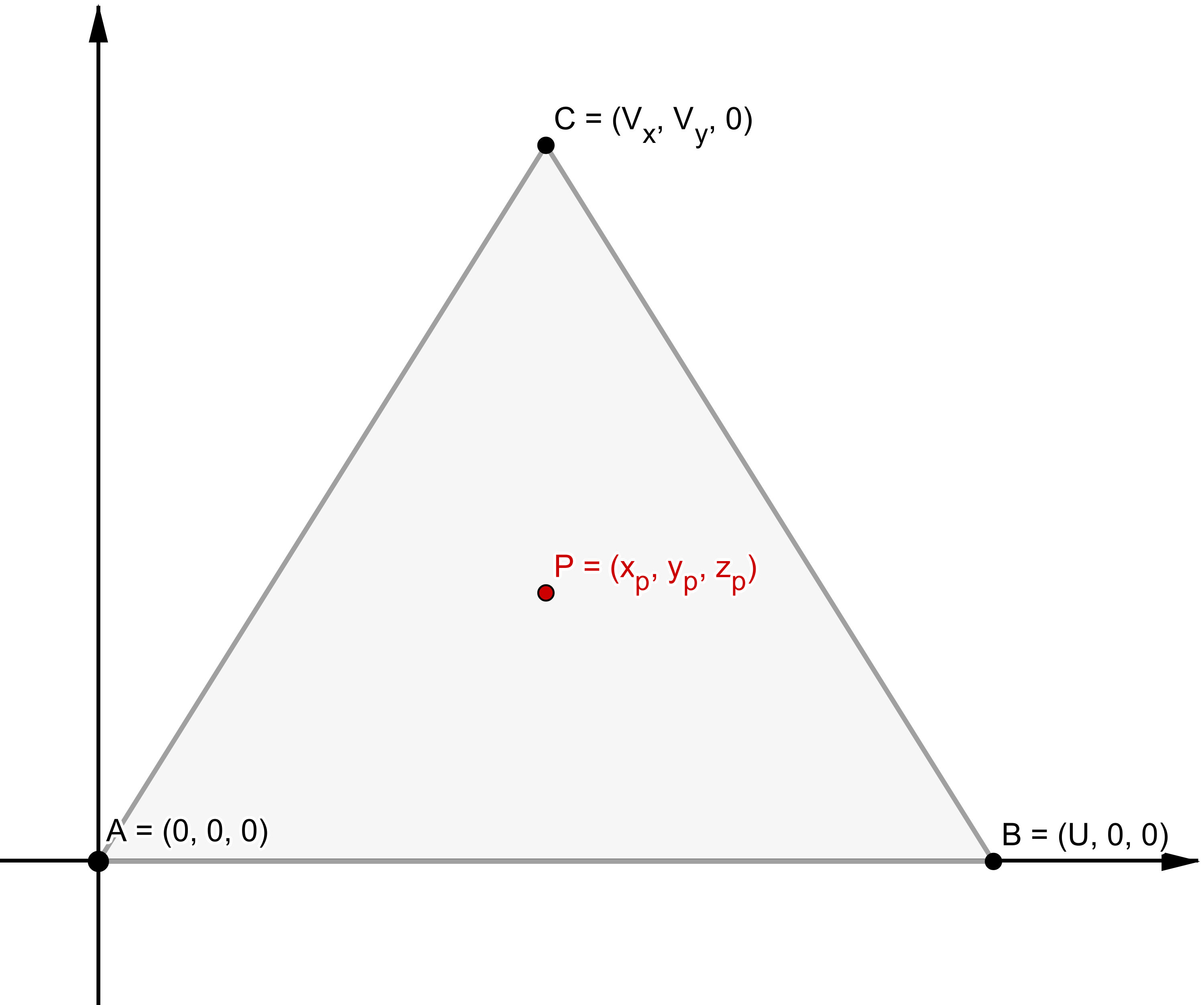
A 2D view of the obtained marker.
In this plane, the coordinates of the point are the following:
If \(z_p\) is equal to zero, then the solution is defined as the following:
Otherwise, if \(z_p\) is strictly superior to zero, then there are two possible solutions; in this case, they are defined as:
There is always one position; otherwise, that might mean that one GPS host is misconfigured or lying.
Coordinates are rounded to .01 blocks.
Todo
Why the rounding to .01? It’s possible this might be thought for turtles because they can request something while moving, although I am not sure what the precision and speed is in this case.
Todo
When there are two possible positions after rounding, then the system
uses the other GPS hosts to fix the position using narrow.
Todo
Classic GPS cluster structure, explain it.
From what has been said on Discord: you can’t have four computers side-by-side for use as GPS host as there would be ambiguous positions. Courtesy to Wojbie for this marvelous diagram:
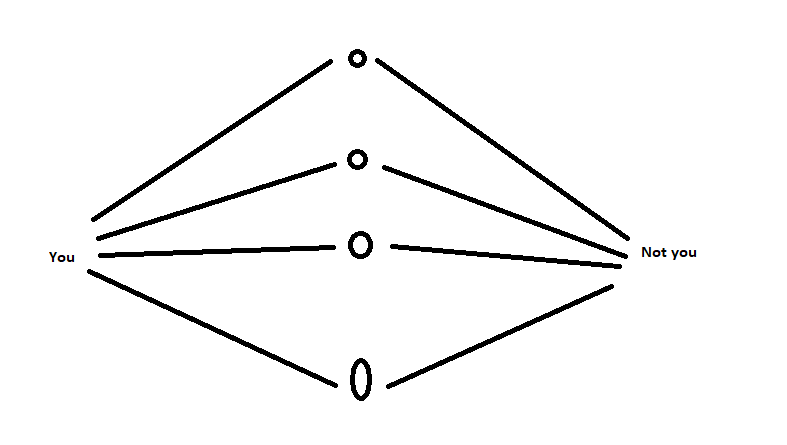
However, that doesn’t explain why the classic GPS cluster structure is as it is:
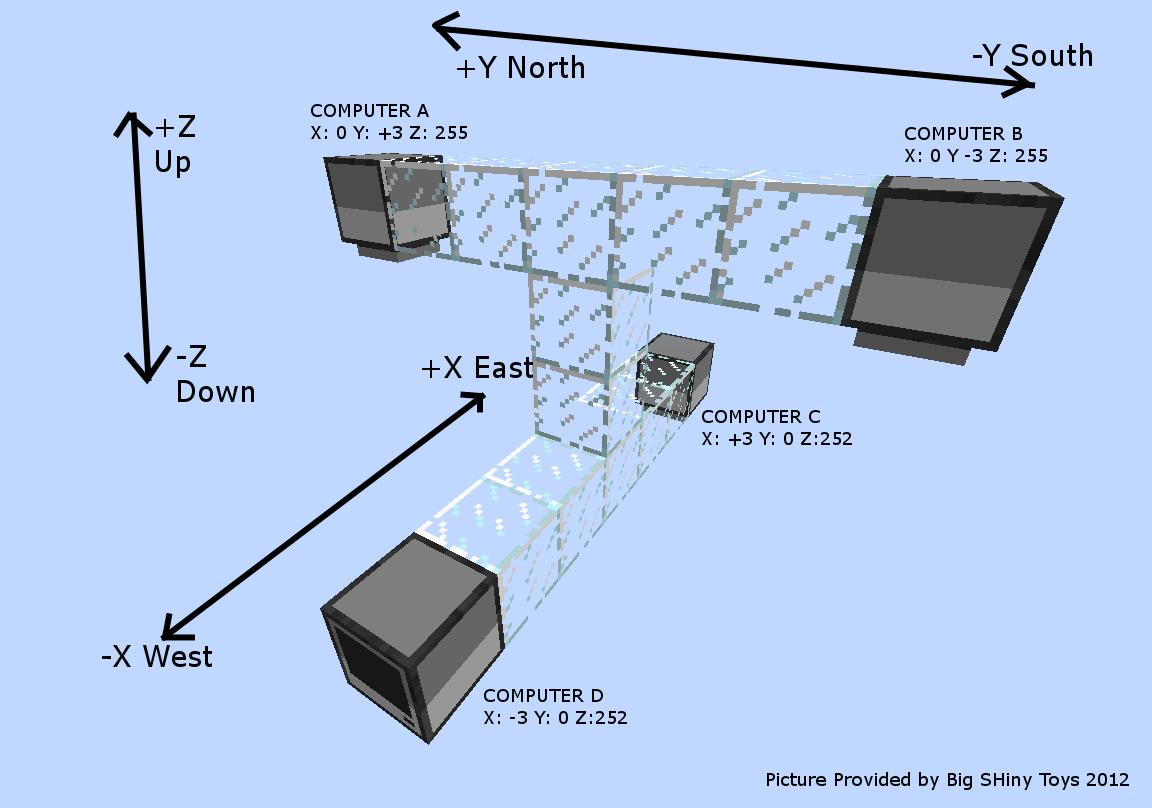
“I’m assuming they’re scattered so that there are at least two computers on different planes for X, Y, and Z” — JackMacWindows
See gps-trilaterate.lua for a Lua implementation of
the trilateration algorithm.